papers_we_read

You Only Train Once : Loss-conditional training of deep networks

Alexey Dosovitskiy, Josip Djolonga, ICLR 2020

Summary

The paper proposes a simple and broadly applicable approach that efficiently deals with multi-term loss functions and, more generally, arbitrarily parameterized loss functions. It suggests a method to train a single model simultaneously minimizing a family of loss functions instead of training a set of per-loss models.

Concept behind the paper

The main concept is to train a single model that covers all choices of coefficients of the loss terms, instead of training a model for each set of coefficients. This is achieved by:

• First: training the model on a distribution of losses instead of a single loss function
• Second: conditioning the model outputs on the vector of coefficients of the loss terms.

This way, at inference time the conditioning vector can be varied, allowing us to traverse the space of models corresponding to loss functions with different coefficients.

Methodology

• Instead of a single fixed loss function L(·, ·), assume that we are interested in a family of losses L(·, ·, λ), parameterized by a vector λ ∈ Λ ⊂ R d λ .

• The most common case of such a family of losses is a weighted sum of several loss terms with weight λ_i corresponding to loss Lⁱ.

• In practice, one then typically minimizes the loss independently for each choice of the parameter vector λ.

• Instead of fixing λ, the paper proposes an optimization problem where the parameters λ are sampled from a distribution P_λ (log-uniform distribution in this paper’s experiments) .

• Hence, during training time the model observes many losses, and can learn to utilize the relationships between them to optimize all of them simultaneously. The distribution P_λ can be seen as a prior over the losses.

• At inference time, the joint model can be conditioned on an arbitrary desired parameter value λ, yielding the corresponding predictions.

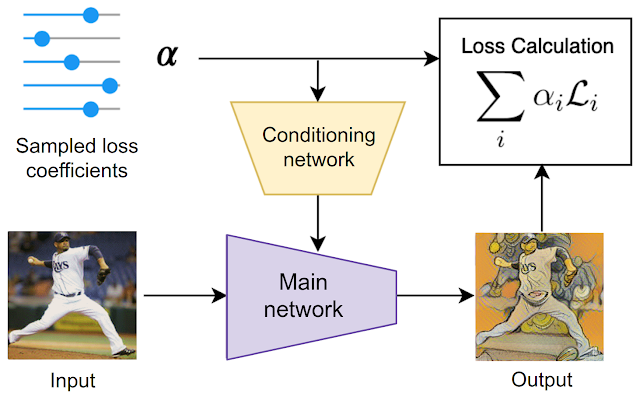
This training procedure is illustrated in the diagram below for the style transfer task:

• For each training example, first the loss coefficients are randomly sampled.
• Then they are used both to condition the main network via the conditioning network and to compute the loss.

Main contributions

• In many ML problems, multiple loss functions have to be minimized simultaneously, each of them modelling a different facet of the considered problem.

• Typically, it is not possible to simultaneously optimize all these losses — either due to limited model capacity, or because some of the losses may be fundamentally in conflict (for instance, image quality and the compression ratio in image compression)

• Intuitively, the models trained for different loss variants are related and could share a large fraction of computation

• The YOTO method helps us to exploit the above fact and train a single model that simultaneously solves several learning tasks.

• The conceptual simplicity of this approach makes it applicable to many problem domains, with only minimal changes to existing code bases.

• The experiments have been carried out on three problems: Beta-VAE, Style Transfer and Learned Image Compression. The results showed close similarity with fixed-weight models trained for each of the parameter configurations.

Our two cents

• Easier Training: YOTO could reduce the effort spend in training models with fixed parameters separately as we won’t have to decide the exact weights ourselves and try out different models (eg. the beta factor for the KL-divergence loss in Beta-VAE).

• Relation between loss factors: Studying the nature of P_λ distribution could help us in better understanding the relation between different losses of a model.

• Depends on capacity of the model: For small-capacity models the proposed method somewhat under-performs relative to the fixed-weight models,since it is difficult for a small model to cover all loss variants. However, as the capacity is increased, YOTO models eventually outperform the fixed-weights models.

• P_λ distribution: It has to be chosen(or rather is picked) at present. It would be interesting to devise provably effective strategies of selecting the loss parameter distribution, especially for losses with multiple parameters.

• Task dependent: It will likely only work on “easier” tasks. On difficult datasets even fitting the model to a fixed loss-factor is hard. It is doubtful if in such situation, the model could generalize to well to arbitrary loss-factors. Also training time and memory are two important factors to be kept in mind.

Resources

• You Only Train Once (Blog)

This site is open source. Improve this page.